ACTIVIDADES PRIMARIA: MATEMÁTICAS

TODAS LAS UNIDADES

CÁLCULO MENTAL

PARA ENTRENAR EL CÁLCULO MENTAL

REPASO TODAS LAS MATEMÁTICAS DE PRIMARIA

REFUERZA Y AMPLIA LAS MATEMÁTICAS(SUMAS, RESTAS, MULTIPLICACIONES Y DIVISIONES)

PROBLEMAS PARA HACER ON LINE

MATEMÁTICAS DIVERTIDAS

USA EL COCO

RELACIONES ENTRE LAS MEDIDAS DE LONGITUD, CAPACIDAD Y MASA

ACTIVIDADES SOBRE LAS MEDIDAS DE LONGITUD

ACTIVIDADES SOBRE LAS MEDIDAS DE CAPACIDAD

ACTIVIDAES SOBRE LAS MEDIDAS DE MASA

CÁLCULO

CÁLCULO MENTAL DE SUMAS Y RESTAS

EVALUACIÓN INICIAL

RECORDAMOS LA PRUEBA DE LA RESTA

REPASO LA TABLA DE MULTIPLICAR

¿TE PREGUNTO LAS TABLAS?

RECUERDO Y REPASO LA DIVISIÓN

RECORDAMOS LOS NÚMEROS ROMANOS

SEGUIMOS PRACTICANDO LOS NÚMEROS ROMANOS

DESCOMPOSICIÓN DE NÚMEROS HASTA LA CENTENA DE MILLÓN

MULTPLICACIÓN DE UN NÚMERO NATURAL POR LA UNIDAD SEGUIDA DE CEROS

ESCRIBIR NÚMEROS

PIENSA Y ESCRIBE LOS NÚMEROS

ORDENA GRUPOS DE NÚMEROS

UNIDAD 1:OPERACIONES CON NÚMEROS NATURALES

DIVISIONES DE NÚMEROS NATURALES

MULTIPLICACIÓN Y DIVISIÓN POR LA UNIDAD SEGUIDA DE CEROS

UNIDAD 2:OPERACIONES CON NÚMEROS DECIMALES

APRENDO A SUMAR Y RESTAR CON DECIMALES
REPASO LA SUMA CON DECIMALES

REPASO LA RESTA CON DECIMALES

OPERACIONES CON NÚMEROS DECIMALES

REPASO LA MULTIPLICACIÓN CON NÚMEROS DECIMALES

MULTIPLICACIONES CON NÚMEROS DECIMALES

MULTIPLICACIÓN POR LA UNIDAD SEGUIDA DE CEROS CON DECIMALES
MULTIPLICACIÓN DE UN NÚMERO NATURAL POR UNO DECIMAL

MULTIPLICO UN NÚMERO DECIMAL POR LA UNIDAD SEGUIDA DE CEROS

UNIDAD 3:DIVISIÓN DE NÚMEROS DECIMALES

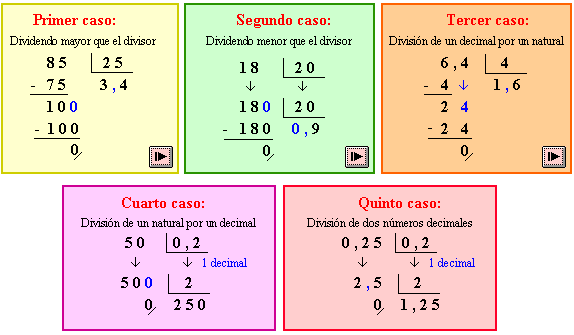
DIVISIÓN DE UN NÚMERO DECIMAL ENTRE UN NÚMERO DECIMAL

DIVISIÓN DE NÚMEROS DECIMALES

APRENDO COMO SE HACEN LAS DIVISIONES CON DECIMALES

DIVISIÓN DE UN NÚMERO DECIMAL ENTRE UNO NATURAL

DIVISIÓN DE UN NÚMERO NATURAL ENTRE UN NÚMERO DECIMAL

DIVISIÓN DE UN NÚMERO DECIMAL ENTRE OTRO DECIMAL

DIVISIÓN ENTRE LA UNIDAD SEGUIDA DE CEROS CON DECIMALES

DIVISIÓN DE UN NÚMERO NATURAL ENTRE LA UNIDAD SEGUIDA DE CEROS

DIVISIÓN DE UN NÚMERO DECIMAL ENTRE LA UNIDAD SEGUIDA DE CEROS

REPASAMOS LAS DIVISIONES DE NÚMEROS DECIMALES

UNIDAD 4: MÚLTIPLOS Y DIVISORES

EXPLICACIÓN Y EJERCICIOS SOBRE LOS MÚLTIPLOS

Más ejericios sobre múltiplos

EXPLICACIÓN Y EJERCICIOS SOBRE LOS DIVISORES

Más ejercicios sobre divisores

¿Reconozco divisores?

Problemas sobre múltiplos y divisores

Reconocer múltiplos y divisores con ayuda de la calculadora

------------------------------------------------------------------------------------------------------------

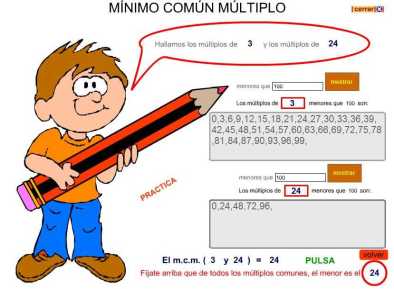
EXPLICACIÓN Y ACTIVIDADES DEL M.C.M

ACTIVIDADES DEL M.C.M

APLICACIÓN DEL M.C.M A PROBLEMAS

MÚLTIPLOS COMUNES A VARIOS NÚMEROS

------------------------------------------------------------------------------------------------------------

APRENDEMOS A CALCULAR EL M.C.D

OTRA EXPLICACIÓN DEL M.C.D

ACTIVIDAD DE MÁXIMO COMÚN DIVISOR

JUEGO SOBRE EL M.C.D

----------------------------------------------------------------------------------------------------------- EXPLICACIÓN DE NÚMEROS PRIMOS Y COMPUESTOS

ACTIVIDAD SOBRE NÚMEROS PRIMOS

DIFERENCIA LOS NÚMEROS PRIMOS DE LOS COMPUESTOS
------------------------------------------------------------------------------------------------------------

CRITERIOS DE DIVISIBILIDAD DE 2, 3, 5, 9 Y 10

PRACTICO LAS REGLAS DE DIVISIBILIDAD

JUEGOS PARA PRACTICAR LOS CRITERIOS DE DIVISIBILIDAD

EJERCICIOS PARA PRACTICAR LOS CRITERIOS DE DIVISIBILIDAD

MÁS EJERCICIOS SOBRE LOS CRITERIOS DE DIVISIBILIDAD

------------------------------------------------------------------------------------------------------------

AUTOEVALUACIÓN DEL TEMA 4

-----------------------------------------------------------------------------------------------

UNIDAD 5: POTENCIAS Y RAÍCES

¿QUÉ ES UNA POTENCIA?

APRENDEMOS POTENCIAS

REPASAMOS EL CONCEPTO DE POTENCIA

APRENDO EL CUADRADO DE UN NÚMERO NATURAL

EL CUADRADO Y EL CUBO DE UN NÚMERO NATURAL

PRACTICO LAS POTENCIAS AL CUADRADO

¿QUÉ ES EL CUBO DE UN NÚMERO NATURAL?

NÚMEROS NATURALES AL CUBO

PRACTICO LAS POTENCIAS AL CUBO

POTENCIAS COMO PRODUCTOS DE FACTORES IGUALES

EJERCICIOS DE POTENCIAS

PRACTICO LAS POTENCIAS

JUEGO CON LAS POTENCIAS AL CUDARDO Y AL CUBO

PRACTICO LAS POTENCIAS

APRENDO A LEER POTENCIAS

APRENDO A LEER POTENCIAS 2
...........................................................................................................................................

APRENDO LAS POTENCIAS DE BASE 10

APRENDO A EXPRESAR NÚMEROS CON POTENCIAS DE BASE 10

¿CUÁL SON ESTOS NÚMEROS NATURALES EXPRESADOS EN POTENCIAS DE BASE 10?
POTENCIAS DE BASE 10

AFIANZAMOS LO APRENDIDO

........................................................................................................................................

¿QUÉ ES UNA RAÍZ CUADRADA?

ENTENDEMOS EL CONCEPTO DE RAÍZ CUADRADA

¿CÓMO CALCULO LAS RAÍCES CUADRADAS?

EJERCICIOS DE RAÍCES CUADRADAS

PRACTICO LAS RAÍCES CUADRADAS

RESUELVO PROBLEMAS DE RAÍCES CUADRADAS

PROBLEMAS DE RAÍCES CUADRADAS

......................................................................................................................................

AUTOEVALUACIÓN DE TEMA 5

AUTOEVALUACIÓN 2 DEL TEMA 5

AUTOEVALUACIÓN 3 DEL TEMA 5

AUTOEVALUACIÓN 4 DEL TEMA 5

........................................................................................................................................
REPASODEL PRIMER TRIMESTRE

........................................................................................................................................

UNIDAD 6: LAS FRACCIONES

EXPLICACIÓN DEL TEMA:

FRACCIONES

La fracción se utiliza para representar las partes que se toman de un objeto que ha sido dividido en partes iguales.
Por ejemplo, dividimos una pizza en 8 partes iguales y cogemos tres. Esto se representa por la siguiente fracción:

Los términos de la fracción se denominan: numerador y denominador.

¿Cómo se leen las fracciones? Se leen en función de cuál es su denominador:

1 / 2: un medio
1 / 3: un tercio
1 / 4: un cuarto
1 / 5: un quinto
1 / 6: un sexto
1 / 7: un séptimo
1 / 8: un octavo
1 / 9: un noveno
1 / 10: un décimo
1 / 11: un onceavo
1 / 12: un doceavo
1 / 13: un treceavo
Veamos algunos ejemplos:

¿A cuantas unidades equivale una fracción? Para calcularlo se divide el numerador entre el denominador:

Por ejemplo:

Para ver a cuantas unidades equivale esta fracción dividimos: 2 : 8 = 0,25

Equivale a 0,25 unidades

Si una fracción tiene igual numerador y denominador representa la unidad.

Por ejemplo, divido una tarta en 4 partes y me tomo las cuatro partes:

Qiere decir que me he tomado la totalidad de la tarta. (4 / 4) equivale a la unidad (a la tarta). Si dividimos 4 : 4 = 1

1.- Fracciones equivalentes
Dos fracciones son equivalentes cuando equivalen a las mismas unidades.
Por ejemplo:

Estas dos fracciones son equivalente ya que equivalen a las mismas unidades:

4 : 8 = 0,5 unidades
1 : 2 = 0,5 unidades
¿Cómo sabemos cuando dos fracciones son equivalentes?
Para ello dividimos sus numeradores y sus denominadores, si guardan la misma proporción es que son equivalente:
Veamos un ejemplo:

Dividimos sus numeradores: 6 : 2 = 3

Dividimos sus denominadores: 9 : 3 = 3

Guardan la misma proporción (3) luego estas dos fracciones son equivalentes.

Podemos comprobarlo.

La primera fracción equivale a 6 : 9 = 0,66 unidades

La segunda fracción equivale a 2 : 3 = 0,66 unidades

Veamos ahora un ejemplo de dos fracciones que no son equivalentes:

Dividimos sus numeradores: 2 : 3 = 0,66

Dividimos sus denominadoress: 4 : 9 = 0,44

No guardan la misma proporción luego estas dos fracciones no son equivalentes.

Podemos comprobarlo.

La primera fracción equivale a 2 : 4 = 0,50 unidades

La segunda fracción equivale a 3 : 9 = 0,33 unidades

2.- Comparación de fracciones
¿Cómo puedo saber si una fracción es mayor o menor que otra?
Para ello vamos a distinguir:

Comparar fracciones con el mismo denominador
Comparar fracciones con distinto denominador

a) Comparar fracciones con el mismo denominador
Es mayor la fracción que tenga mayor el numerador.

Podemos comprobar que 2 / 4 = 0,5 mientras que 1 / 4 = 0,25, luego la primera fracción es mayor.

También podemos comprobar que 5 / 9 = 0,55 mientras que 3 / 9 = 0,33, luego la primera fracción es mayor.

b) Comparar fracciones con distinto denominador
En este caso puede ocurrir que tengan el mismo numerador o no.
b.1.- Si tienen el mismo numerador es mayor la que tenga menor denominador.

En este caso comprobamos que 8 / 3 = 2,66 mientras que 8 / 5 = 1,60, luego la primera fracción es mayor.

También podemos ver que 6 / 2 = 3,00 mientras que 6 / 4 = 1,50, luego la primera fracción es mayor.

b.2.- Si tienen distinto numerador entonces para poder comparalas hay que expresarlas con el mismo denominador:

Si los dos términos de una fracción se multiplican por el mismo número la fracción resultante es equivalente.
¿Y por qué número multiplicamos cada fracción? la primera fracciónla multiplicamos por el denominador de la segunda, y la segunda por el denominador de la primera.
Veamos un ejemplo:

Para comparar estas dos fracciones, vamos a multiplicar los dos términos de la primera fracción por 2 (denominador de la segunda).

Podemos comprobar que al multiplicar numerador y denominador por el mismo número la fracción no cambia: 3 / 7 = 0,428 mientras que 6 / 14 = 0,428.
Y vamos a multiplicar los dos términos de la segunda fracción por 7 (denominador de la primera).

Ahora las dos fracciones ya tienen el mismo denominador, luego podemos compararlas:

Vemos que la segunda fracción es mayor que la primera porque su numerador es mayor